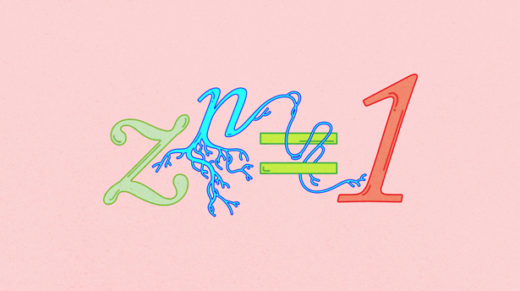Unraveling the Mysteries of Mathematical Eternity
A Glimpse into the Infinite
In the realm of mathematical enigmas, few have captivated and confounded scholars as profoundly as Fermat’s Last Theorem. With its origins dating back to 17th-century France, this tantalizing puzzle has beckoned mathematicians across generations with promises of elusive truths hidden within its intricate folds.
Like a symphony composed by an unseen maestro, Pierre de Fermat’s theorem dances on the precipice between certainty and conjecture. Its essence lies in a seemingly simple equation: x^n + y^n = z^n. Yet beneath this elegant facade lies a labyrinthine journey that has consumed countless minds throughout history.
For centuries, mathematicians grappled with this riddle, their pens scratching feverishly against parchment in pursuit of enlightenment. However, it was not until 1994 that Andrew Wiles emerged from his intellectual seclusion to present what appeared to be an almost-proof—a glimmering beacon amidst the foggy expanse of uncertainty.
An Ode to Persistence
Woven into the fabric of Wiles’ proof is a testament to human resilience and unwavering dedication—an ode to those who dare challenge the boundaries imposed upon them by nature itself. Like an artist meticulously crafting each brushstroke or a poet laboring over every syllable, Wiles embarked on an arduous quest through uncharted mathematical terrain.
Inspired by ancient texts and guided by intuition honed through years spent immersed in numbers’ ethereal embrace, he traversed treacherous landscapes where others had faltered before him. Armed with intellect sharpened like Damascus steel and a spirit unyielding in the face of adversity, Wiles ventured into the depths of mathematical infinity.
His journey was not without its perils. The path he treaded was strewn with obstacles—false starts and dead ends that threatened to derail his pursuit. Yet, undeterred by these setbacks, Wiles pressed on, driven by an insatiable hunger for knowledge and an unwavering belief in the beauty hidden within Fermat’s Last Theorem.
A Glimmer of Truth
As if touched by divine inspiration, Wiles’ almost-proof illuminated the mathematical firmament like a supernova—a fleeting glimpse into a world where numbers dance harmoniously in perfect symphony. His labyrinthine odyssey had led him to uncover profound connections between elliptic curves and modular forms—an intricate tapestry woven from threads spanning centuries.
Yet, despite this monumental breakthrough, whispers of doubt lingered amidst the jubilation. Like shadows cast upon a sunlit meadow, questions arose regarding certain assumptions made along Wiles’ arduous journey. And so began another chapter in the ever-evolving saga of Fermat’s Last Theorem—a testament to humanity’s ceaseless quest for truth.
The Unquenchable Thirst
In conclusion, while Andrew Wiles’ almost-proof tantalizes us with its brilliance and elegance, it serves as a reminder that even within realms seemingly boundless and infinite lies an insatiable thirst for understanding—the eternal yearning to unlock secrets hidden deep within nature’s embrace. As we continue our exploration into mathematical enigmas such as Fermat’s Last Theorem, let us be guided by curiosity and tenacity—ever seeking answers that lie just beyond our grasp but forever beckon us forward on this captivating voyage through intellectual discovery.